dan persamaan radialnya (Persamaan 4.37) adalah

Tantangan kita kali ini adalah menyelesaikan persamaan ini untuk u(r) dan menghitung energi elektron E yang diijinkan. Atom hidrogen adalah sebuah kasus penting dalam mekanika kuantum yang mana kita akan menyelesaikannya secara detail dengan menggunakan metode yang telah digunakan dalam solusi analitik pada permasalahan osilator harmonik. (Jika setiap lagkah dalam proses ini kurang jelas, kamu bisa melihat kembali pada sesi 2.3.2 untuk penjelasan lebih lengkap.) Kebetulan sekali, potensial Coulomb berlaku keadaan kontinu (dengan E > 0), yang menjelaskan hamburan elektron-proton, sebaik pada keadaan terikat diskret, yang merepresentasikan atom hidrogen, tetapi sebaiknya kita menahan perhatian kita mengenai hal ini untuk dibahas kemudian.
4.2.1 Fungsi Gelombang Radial
Tugas pertama kita adalah untuk merapikan notasi. Kita misalkan
(Untuk keadaan terikat, E < 0, maka
Dengan ini dianjurkan untuk memisalkan dengan
Dengan permisalan tersebut, maka persamaan radial menjadi
Selanjutnya kita memanfaatkan bentuk asimtotik dari solusi. pada
Dari sini, solusi umumnya adalah
tetapi, nilai
untuk nilai
Solusi umumnya adalah (kamu bisa memeriksanya sendiri)
Tetapi  bernilai tak berhingga pada
bernilai tak berhingga pada 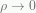 , maka kita harus memilih
, maka kita harus memilih 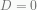 . Oleh karena itu
. Oleh karena itu
untuk nilai
Langkah selanjutnya adalah menghilangkan perilaku asimptotik, untuk itu kita perkenalkan fungsi baru  :
:
Dengan harapan bahwa
dan turunan keduanya adalah
Dalam bentuk  , maka persamaan radial menjadi
, maka persamaan radial menjadi
Akhirnya, kita bisa mengasumsikan bahwa solusi
Permasalahan kita sekarang adalah untuk menentukan koefisien
[Dalam penjumlahan kedua kita telah menamakan ulang “indeks durni”: 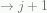 . Jika ini mengganggumu, tulislah ulang penjumlahan yang pertama secara lebih eksplisit, dan periksalah. Kamu mungkin berkata kalau penjumlahan seharusnya dimulai pada
. Jika ini mengganggumu, tulislah ulang penjumlahan yang pertama secara lebih eksplisit, dan periksalah. Kamu mungkin berkata kalau penjumlahan seharusnya dimulai pada 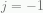 , tetapi faktor
, tetapi faktor  dapat menghilangkan permasalahan tersebut, sehingga kita bisa memulai penjumlahan sama seperti biasanya yaitu dimulai pada
dapat menghilangkan permasalahan tersebut, sehingga kita bisa memulai penjumlahan sama seperti biasanya yaitu dimulai pada 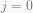 .] Penurunan lagi terhadap
.] Penurunan lagi terhadap  ,
,
Dengan memasukkan ini ke dalam Persamaan 4.61 kita dapatkan
Dengan menyamakan koefisiennya berdasarkan pagkatnya menghasilkan
atau
Rumusan rekursi ini menentukan nilai koefisien, dan karena itu fungsi
Sekarang, kita lihat seperti apa bentuk koefisiennya untuk nilai j yang besar (ini berhubungan dengan nilai  yang besar pula, di mana didominasi oleh pangkat yang terbesar). Dalam daerah ini, formula rekursi menjadi
yang besar pula, di mana didominasi oleh pangkat yang terbesar). Dalam daerah ini, formula rekursi menjadi
sehingga
Untuk saat ini anggap saja ini adalah solusi eksaknya. Maka
dan oleh sebab itu
yang akan menjadi tak berhingga pada
(dan koefisien yang berada diluar ini akan hilang dengan sendirinya). Dengan jelas
Definisikan
(yang dinakamakan dengan bilangan kuantum utama), kita punya
Karena
maka energi yang diijjinkan adalah
Ini adalah formula Bohr yang terkenal-hasil yang paling penting dari setiap pengukuran dalam mekanika kuantum. Bohr mendapatkannya pada 1913 yang mana tidak dapat diterapkan dalam fisika klasik dan awal-awal kelahiran teori kuantum (Persamaan Shroedinger belum muncul hingga tahun 1924).
Pengkombinasian Persamaan 4.55 dan 4.68 kita dapatkan bahwa
di mana
adalah jari-jari Bohr. Ini berlanjut bahwa
Dengan jelas bahwa fungsi gelombang spasial untuk atom hodrogen ditandai dengan tiga bilangan kuantum (n, l, dan m):
di mana
dengan
Keadaan dasarnya (ground state) adalah pada
Dengan jelas energi ikat atom hidrogen (nilai energi yang harus diberikan pada elektron untuk mengionisasi atom) adalah 13,6 eV. Persamaan 4.67 menghendaki
Formula rekursi terpotong setelah bagian yang pertama dengan 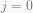 menghasilkan
menghasilkan 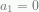 ), sehingga
), sehingga  adalah sebuah konstanta (
adalah sebuah konstanta (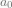 ) dan
) dan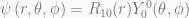 .
.
Dengan menormalisasikannya, yang sesuai dengan Persamaan 4.31,
sehingga 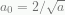 . Sementara itu,
. Sementara itu, 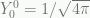 , maka
, maka
Jika
Ini adalah keadaan tereksitasi yang pertama, atau baiknya, suatu keadaan dimana kita memiliki
Maka  , dan karenanya
, dan karenanya
Jika
pada setiap kasus
Untuk sembarang 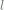 , nilai
, nilai 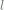 yang mungkin adalah konsisten
yang mungkin adalah konsisten
Untuk masing-masing
Polynomial
di mana ,
,
adalah polynomial Laguerre terasosiasi, dan
adalah polynomial Laguerre ke-q.[3] (beberapa polynomial ditampilkan dalam Tabel 4.4. beberapa polynomial Laguerre terasosiasi diberikan dalam Tabel 4.5. Beberapa fungsi gelombang radial ditampilkan dalam Tabel 4.6 dan sketsa grafiknya dapat dilihat dalam Gambar 4.4.) Normalisasi fungsi gelombang atom hydrogen adalah[4]
Sebenarnya ini tidaklah mencerminkan keadaan nyata secara benar, tetapi Ini adalah salah satu dari beberapa sistem yang paling realistis yang dapat diselesaikan hingga saat ini dalam bentuk yang eksak. Itu juga bersifat orthogonal yang akan kita buktikan kemudian



no coment
BalasHapus